

第1页 / 共20页

第2页 / 共20页

第3页 / 共20页

第4页 / 共20页
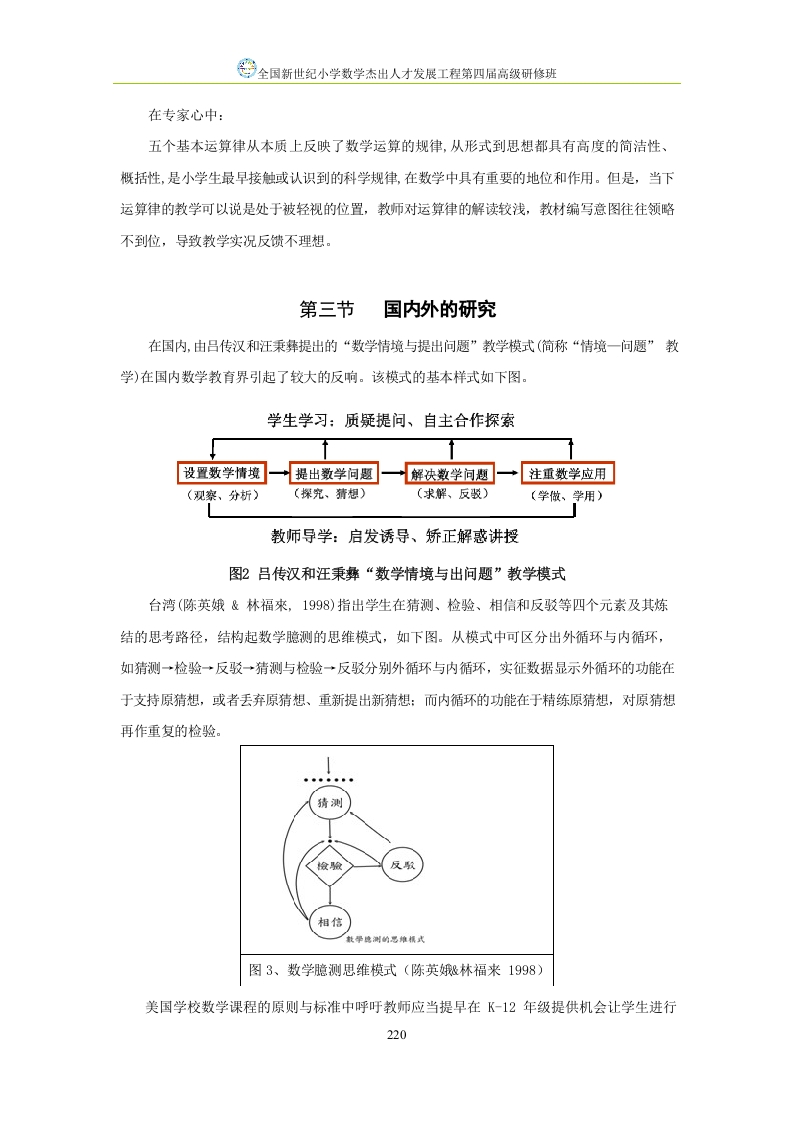
第5页 / 共20页
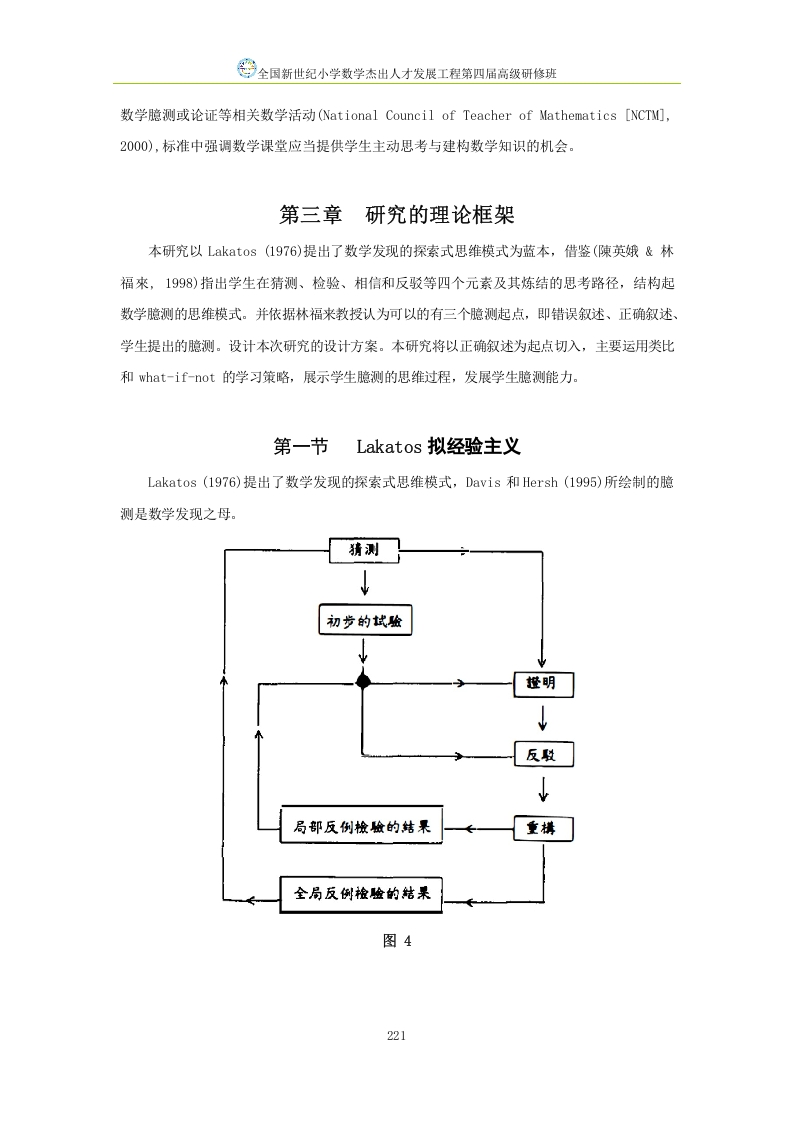
第6页 / 共20页
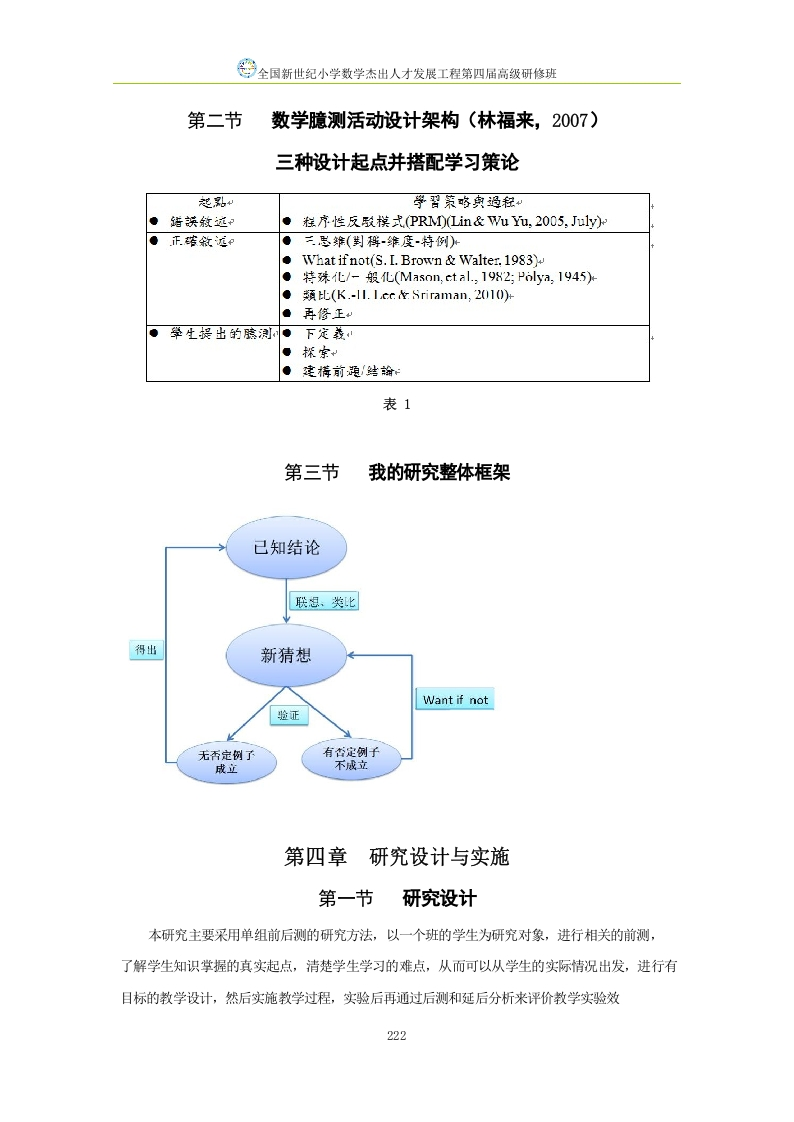
第7页 / 共20页
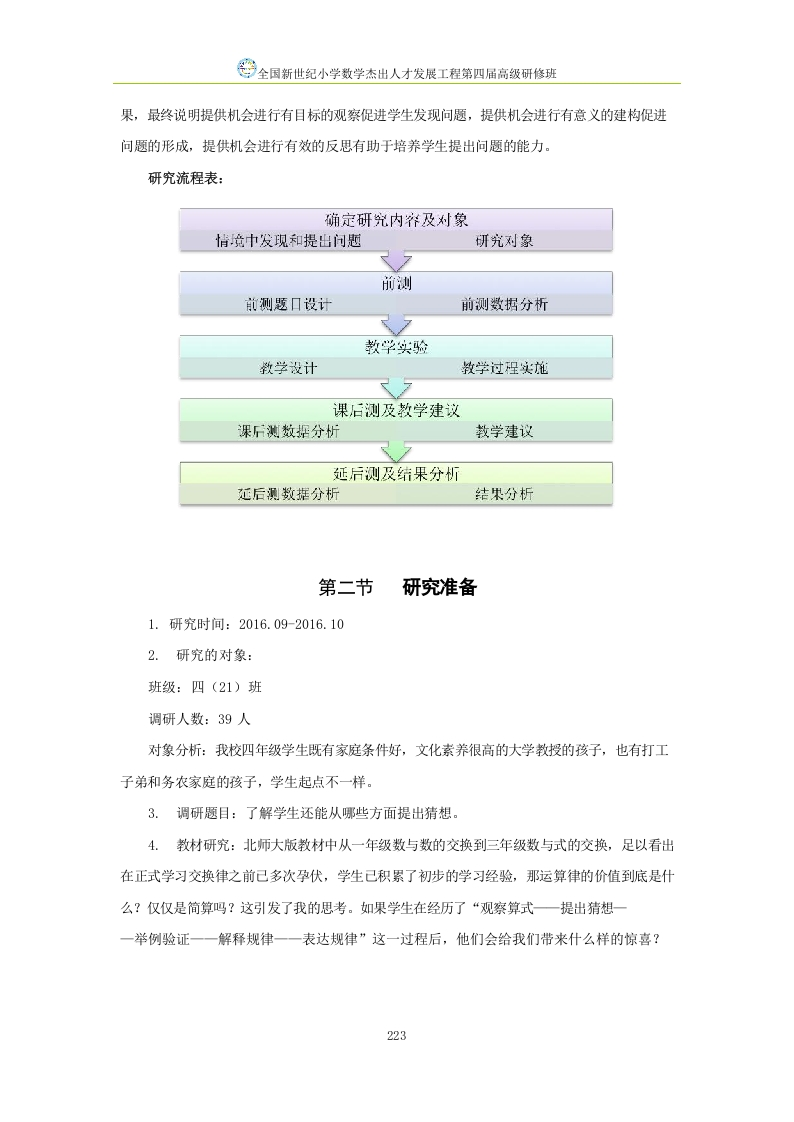
第8页 / 共20页
试读已结束,还剩12页,您可下载完整版后进行离线阅读
由加法交换律切入提出猜想发展臆测能力此内容为付费资源,请付费后查看
黄金会员免费钻石会员免费
付费资源
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
等全国新世纪小学数学杰出人才发展工程第四届高级研修班第一章课题的背景第一节研究缘起1.新课程目标的提出随着《数学课程标准(2011)》的课程目标由“双基”到“四基”,能力要求也新增了两个能力,即发现问题的能力和提出问题的能力。史宁中老师:发现问题与培养学生的创新意识关系密切,而提出问题与培养学生的创新能力关系密切。看来,运用数学的思维方式进行思考,增强学生不断发现问题、提出问题,分析问题并解决问题的能力,人们己逐渐达成共识。另外,“以问题作为教学的出发点”,“问题是激起学生思维的最好方式和起点”,“问题是数学的心脏”,“问题让学习发生”等等提法,也足以看出“问题“能引发学生主动思考,本研究中提到的猜想正是课标中强调的让学生经历发现问题、提出问题、分析问题、解决问题全过程中的一个环节。2.教材中的内容引发的思考北师大版教材中从一年级数与数的交换到三年级数与式的交换,足以看出在正式学习交换律之前己多次孕伏,为“猜想”提供了更广阀的背景和可能,学生己积累了初步的学习经验,那运算律的价值到底是什么?仅仅是简算吗?应从对结果的关注一到对式的关系的研究,经历“观察算式一提出猜想—举例验证—解释规律—表达规律一从结论切入一提出新猜想”这一过程后,他们会给我们带来什么样的惊喜,值得期待。第二节研究的目的与意义根据教学经验及听课感受,我们发现学生在课堂上大部分时间都是在回答老师的问题,与老师的思路保持高度一致。很少看到学生能主动提出问题,能提出一个猜想就更难一求了。故本课题将在课堂实践中进行,让学生从一个结论切入,提出一个可能是对的,但尚未证实的数学叙述或数学命题,即前面提到的猜想。虽然大多数猜想并非正确或需修正,但却是数学思考的核心或骨干(Mason,etal.,1982),具有启动与延续数学思考的功能,同时也是通往概念了解、程序流畅、问题解决和合情推理等数学能力的枢纽。因此,从某一结论切入提出猜想这一活动,能促进学生主动思考。另外,在本课题研究是从一个结论切入,积极鼓励学生敢于在课堂上大胆提出提出猜想,教师要精心启发,热情鼓励,学生从多角度提出猜想。并及时与学生回顾和反思,发现如何2

















暂无评论内容